[Pro][삼성] 15942번 : 외계인 침공 - 2
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
지난 포스팅 요약
지난 포스팅에서는 이 문제의 핵심인 "동원을 최소화하기 위해, 침략 순서를 어떻게 정할 것인가?"를 정하는 방법에 대해서 다뤘습니다. 아래 과정을 통해서 동원을 최소화할 수 있었고, 이는 Upper Bound 알고리즘을 활용하여 구현할 수 있었습니다.
1. 모든 행성 정복에 필요한 함선 수를 계산한다. (= 모든 행성의 인원 수를 더한다.)
2. "현재 함선 수 이하의 주민이 있는 행성 중, 가장 주민이 많은 행성"을 고른다.
3. "침략"을 진행한 뒤, 함선이 더 필요한 경우에 "동원" 한다.
3. 1번 과정과 동일하게, 다음으로 침략할 행성을 고른다.
4. 반복한다.
보다 자세한 내용이 궁금하시면, 아래 포스팅을 참고해주세요.
[Pro][삼성] 15942번 : 외계인 침공 - 1
삼성 SWEA 15942 : 외계인 침공 SW Expert Academy SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요! swexpertacademy.com [풀이 후기] 난이도 : ★★★☆ (Pro) 문제 종류 : Sort & Binary Sear
dongdoridong.tistory.com
효율적인 Visited 처리
이전 포스팅 마지막에서는, Upper Bound를 통해 "침략"할 행성 번호를 찾아야 합니다. 만약에 이미 "침략"을 진행한 경우, 그다음 행성을 찾아야 하는데요. visited[ i ] = 1로 표시를 하고, 아래 코드처럼 한칸씩 검사를 해야 한다면, 최악의 경우, N만큼의 while 반복문 실행이 계속될 것이므로, 다른 방법이 필요합니다. 따라서, 오늘은 효율적인 Visited 처리에 대해서 알아보도록 하겠습니다.
int p = upperBound(K) - 1;
while (visited[p]) p--;
다음에 가야할 행성의 위치를 기록해 놓자
N = 7, K = 2일 때를 예로 들으면서, 어떤 방식으로 다음에 가야 할 행성의 위치를 기록하면 되는지 확인해 보겠습니다.
이전 포스팅에서 활용했던, A[ ] 배열(행성 번호와 행성별 인원수를 기록한 배열)과 더불어, pa[ ] 배열(다음으로 방문해야 할 행성 번호를 기록한 배열)을 추가로 아래와 같이 Setting 하여 사용하도록 하겠습니다.
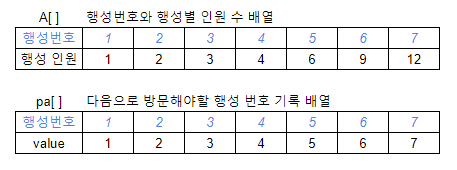
K이하의 주민이 있는 행성 중, 가장 주민이 많은 행성을 먼저 방문하므로, 아래와 같이 4번의 "침략"과 "동원"을 진행하게 됩니다. 이때, pa[ ]의 값은 "방문한 행성 번호(p) - 1"로 업데이트하면 됩니다. 아래 그림 중, 3회 차의 pa[5]는 4가 아니라 3으로 값을 업데이트했는데요. 4번 행성은 이미 방문한 기록이 있으므로, pa [4]=3을 pa[5]에 기록하게 됩니다.

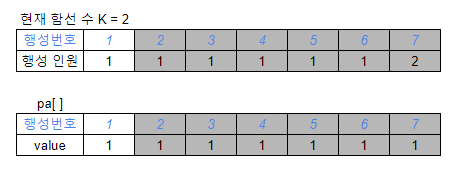
위의 4회차 "침략" & "동원"이 끝나게 되면, 아래의 왼쪽과 같은 상황이 만들어집니다. 다음에 방문해야할 행성 번호는 K=26이므로, 7번 행성인데요. 이미 방문한 기록이 있으니, 6번 행성을 방문하면 됩니다. 이때, 우리는 어떻게 6번 행성을 방문해야할 것을 알 수 있을까요?? 바로 pa[7]에 6번 행성으로 가라는 기록을 남겨두었기 때문에, 오른쪽 그림처럼, 곧장 6번행성으로 갈 수 있게 됩니다.

위와 같은 방법은, 아래와 같은 상황에서 더욱더 큰 효과를 발휘합니다. K=2 이기 때문에, 7번 행성을 방문해야합니다. 기존의 방법대로라면, 6번 행성, 5번 행성, 차례대로 visited 체크를 확인해야합니다. 하지만, 이 방법을 이용하면, 7번 행성이 이미 방문했을 때, 바로 pa[7]을 참조하여, 1번 행성으로 가야함을 알 수 있습니다.
이렇게 "다음에 가야할 행성 위치를 기록"하는 방법은 아래 함수로 구현할 수 있습니다. 재귀(Recursion)를 통해서, 다음에 가야할 행성 위치를 기록하는 방식 입니다.
int find(int pos) {
if (pa[pos] == pos) return pos; // 방문한적 없으면, pos 행성 return
else pa[pos] = find(pa[pos]); // 방문한적 있으면, pa[pos] 위치 기록
}
전체 코드
#include <stdio.h>
#define LM 200000
int N;
int A[LM + 5], trr[LM + 5];
int visited[LM + 5], pa[LM + 5];
void mergeSort(int s, int e) {
if (s >= e) return; // base condition
int m = (s + e) / 2; // divide & conquer
mergeSort(s, m);
mergeSort(m + 1, e);
register int i = s, j = m + 1, k = s; // merge
while (i <= m && j <= e) {
if (A[i] <= A[j]) trr[k++] = A[i++]; // 왼쪽이 남는 경우
else trr[k++] = A[j++]; // 오른쪽이 남는 경우
}
while (i <= m) trr[k++] = A[i++];
while (j <= e) trr[k++] = A[j++];
for (i = s; i <= e; i++) // copy
A[i] = trr[i];
}
int upperBound(int n, long long key) {
int start = 1, end = n, mid;
while (end - start > 0) {
mid = (start + end) / 2;
if (A[mid] <= key)
start = mid + 1;
else
end = mid;
}
return end;
}
int find(int pos) {
if (pa[pos] == pos) return pos; // 방문한적 없으면, pos 행성 return
else pa[pos] = find(pa[pos]); // 방문한적 있으면, pa[pos] 위치 기록
}
int main(void)
{
int test_case;
int T;
scanf("%d", &T);
for (test_case = 1; test_case <= T; ++test_case)
{
long long K, sum = 0;
int ret = 0;
scanf("%d %lld", &N, &K);
for (register int i = 1; i <= N; i++) {
scanf("%d", A + i);
sum += A[i]; // 침략에 필요한 함선 수
visited[i] = 0;
pa[i] = i;
}
mergeSort(1, N);
while (sum > K) {
int p = upperBound(N + 1, K) - 1; // p = K이하 중 가장 큰 수의 Index
if (p > 0) {
p = find(p); // p행성을 방문한적 있다면, 다른 Index 찾기
if (visited[p]) {
ret = -1; break;
}
K += A[p]; // 함선 동원
sum -= A[p]; // 침략
ret++; // 동원 횟수++
visited[p] = 1;
if (p) pa[p] = find(p - 1); // pa[p]에 pa[p-1] 값 기록하기
}
else {
ret = -1; break;
}
}
printf("#%d %d\n", test_case, ret);
}
return 0;
}
제출 결과

참고할만한 포스팅
[알고리즘][탐색][C/C++] Lower Bound, Upper Bound
[알고리즘][탐색][C/C++] Lower Bound, Upper Bound
Lower Bound, Upper Bound 특징 Lower Bound : 원하는 값 k 이상이 처음 나오는 위치를 찾기 Upper Bound : 원하는 값 k 초과가 처음 나오는 위치를 찾기 Binary Search (= 원하는 값 k의 위치 찾기)에서 파생된 index sea
dongdoridong.tistory.com
[알고리즘][정렬][C/C++] Merge Sort (병합정렬)
[알고리즘][정렬][C/C++] Merge Sort (병합정렬)
Merge Sort (병합정렬) 특징 비교를 통해 정렬하는 비교기반 정렬 알고리즘 Divide & Conquer (분할 정복) 알고리즘 시간 복잡도 : O(N*logN) N크기의 임시 배열 1개가 추가적으로 필요 Merge Sort 과정 이해하
dongdoridong.tistory.com